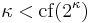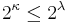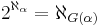Easton's theorem

In set theory, Easton's theorem is a result on the possible cardinal numbers of powersets. Easton (1970) (extending a result of Robert M. Solovay) showed via forcing that

\kappa < \operatorname{cf}(2^\kappa)\,

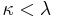and, for \kappa < \lambda\,, that

2^\kappa\le 2^\lambda\,

are the only constraints on permissible values for 2κ when κ is a regular cardinal.

Contents

Statement of the theorem

Easton's theorem states that if G is a class function whose domain consists of ordinals and whose range consists of ordinals such that

  1. G is non-decreasing,
  2. the cofinality of 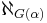\aleph_{G(\alpha)} is greater than 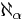\aleph_{\alpha} for each α in the domain of G, and
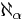  3. \aleph_{\alpha} is regular for each α in the domain of G,

then there is a model of ZFC such that

2^{\aleph_{\alpha}} = \aleph_{G(\alpha)}\,

for each \alpha in the domain of G.

The proof of Easton's theorem uses forcing with a proper class of forcing conditions.

All conditions in the theorem are necessary. Condition 1 is a well known property of cardinality, while condition 2 follows from König's theorem.

No extension to singular cardinals

Silver (1975) proved that a singular cardinal of uncountable cofinality cannot be the smallest cardinal for which the generalized continuum hypothesis fails. This shows that Easton's theorem cannot be extended to the class of all cardinals. The program of PCF theory gives results on the possible values of 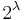2^\lambda for singular cardinals \lambda. PCF theory shows that the values of the continuum function on singular cardinals are strongly influenced by the values on smaller cardinals, whereas Easton's theorem shows that the values of the continuum function on regular cardinals are only weakly influenced by the values on smaller cardinals.

See also

References